TL; DR

glasnsciです。PixInsight（PI）には様々な機能があります。あまりにたくさん機能がありすぎて、一度も使ったことがない関数もあるほどです。「こんな名前しているけど、一体何に使うんだこの関数は？」というものもたくさんあります。そんなある日わたくしは、Processに離散Fourier変換を行なう関数があるのを発見しました。本稿では簡単に結果を紹介します。

Fourier変換復習

Fourier変換とは、ざっくりいうとある関数 $f(t)$ を周波数（波長）空間の関数 $\hat{f(\omega)}$ ないし $\hat{f(\lambda)}$ へ変換するもので、複雑な関数をsin・cosの波で表現しているようなものです。

$\displaystyle \mathcal{F} [ f(t) ] =\hat{f(\omega)}= \frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty} f(t) e^{-i\omega t} dt$

周波数空間に移された関数に逆変換が存在する場合、周波数空間から逆に実数空間に戻すことも可能です。

離散Fourier変換復習

上記の $\mathcal{F} [ f(t) ]$ で表現した式はあくまで連続な関数に対する変換でありますので、現実的な離散値に対しては異なる式を用います。この場合、

$\displaystyle F(\omega) = \sum_{t=0}^{N-1} f(t)\exp\left\lbrace -i\frac{2\pi\omega t}{N} \right\rbrace$

と表現されます。同様に逆変換は

$\displaystyle f(t) = \sum_{\omega=0}^{N-1} F(\omega)\exp\left\lbrace i\frac{2\pi\omega t}{N} \right\rbrace$

上記の離散値に対するFourier変換を離散Fourier変換（Discrete Fourier Transform: DFT）と呼び、逆変換を逆離散Fourier変換（Inverse ‐: IDFT）と呼びます。さらに、そのアルゴリズムを工夫して高速化したものが高速Fourier変換（Fast -: FFT）です。これらは、 $t_1$ 、 $t_2$ 方向に重積分することによって、2次元空間へ拡張することができます（面倒なのでいろんな証明略）。

2次元の離散フーリエ変換は以下のように表現されます。

$\displaystyle F(\omega_1, \omega_2) = \sum^{N-1}_{t_1=0} \sum^{M-1}_{t_2=0} f(t_1,t_2)\exp\left\lbrace -i\frac{2\pi\omega_1 t_1}{N} \right\rbrace \exp\left\lbrace -i\frac{2\pi\omega_2 t_2}{M} \right\rbrace$

さらに逆変換は以下のようにと表現されます。

$\displaystyle f(t_1, t_2) = \sum^{N-1}_{\omega_1=0} \sum^{M-1}_{\omega_2=0} F(\omega_1, \omega_2)\exp\left\lbrace i\frac{2\pi\omega_1 t_1}{N} \right\rbrace \exp\left\lbrace i\frac{2\pi\omega_2 t_2}{M} \right\rbrace$

Fourier変換はさまざまなところで役だっていて、もちろん周波数や波長解析ももちろんのこと、コンピュータトモグラフィ（所謂X線 CTスキャン）など、あるいは望遠鏡の民が大好きな光学の世界にも役立っています。レンズはFourier変換。

PIでDFT

ながながと書いてきましたが、PIのProcessを開くとFourierという項目があります。

プロセスを起動してみます。すごくシンプルですね。

せっかくなので、変換してみましょう。普通なら、Lenaを使うところですが、今回の教材は、偉大な先人に敬意を払ってだいこもんのアイコンになっている「ドクトル」を採用しましょう。

左が強度情報です。どの周波数が強いかを表した画像です。右が位相情報で、周波数のズレを可視化した画像になっています。

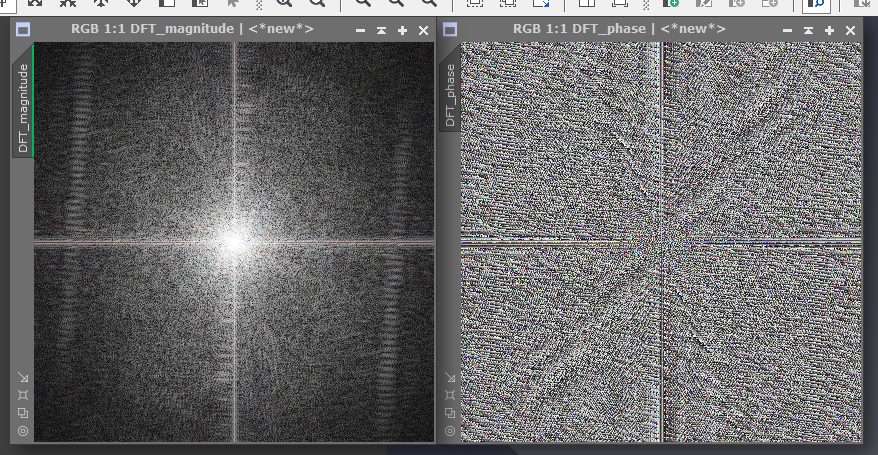
もちろんPIにも逆DFTが存在していて、同じFourierの項目にInverse Fourier Transformがありますので、使ってみましょう。

予想通り、ドクトルが復元されました。

DFTで強度と位相情報に変換されたドクトルと、IDFTによってもとに復元されたドクトル

もちろん、わたくしのアイコンも元に戻せましてよ

周波数フィルタ

GAMEスクリプトで、このように中心にのみ作用するマスクを作ってみましょう。

そして、先程のMagnitudeにマスクのinverseを掛けてHTで周辺の輝度をぐっと上げてみましょう。さらに逆Fourier変換にかけます。ここで重要なのは、PIのDFTで変換された空間が波長空間なのか周波数空間なのか、ということです。いまはただ何も考えずにDFTしただけなので、どのような空間へ変換されたのかわかりません。マスクを掛けてIDFTした結果でその判別が可能ですので、確かめてみましょう。

Magnitudeで周辺の輝度を上げましたので、仮にDFTされた結果が波長空間であれば長波長成分（低周波成分）が強調されて、大きな構造が強調されるでしょう。逆に、周波数空間であれば、高周波成分（短波長成分）が強調されて、ジャギジャギになるはずです。

ジャギジャギになったということで、DFTされた空間は周波数領域だということがわかりました。

おわりに

ところで、PIの制作陣はDFTでなにをさせたかったのでしょう？おそらく上記のような周波数フィルタとしての使用を考えていたのでしょうか。推測の域を出ませんが……。

でもでも、DFTによるフィルタはさまざまなフィルタリングの初歩になっていますので、遊んでみると非常に面白く、皆さんにもぜひ試していただきたいです。普通はOpenCVなどで画像を読み込んで、ソースコードを書いてフィルタリングを色々と行わないと行けないのですが、PIは画像を直接いじることができるので非常に直感的で原理を理解しやすいと思います。ぜひ、遊んで楽しんでもらいたいです。

以上。

ろ座矮小銀河

PixInsightで2D‐DFT/IDFTができるらしい。